The Hexagonal Game of Life
Introduction
Recently on the Purple OSR Discord, PolarFrosty and I have been batting around the idea of using cellular automata in order to proceduralize magic in a game world. The "rules" of a given cellular automata game (the rules to Conway's Game of Life, for example) can be learned diegetically by observation from the people in a given world. If you can learn the rules of reality, you can exploit them!
PolarFrosty's post is about using the specifics of cellular automata to generate world geography and places of magical significance. I wanted to try and use CGOL to tie the way in which wizards recharge their magic to geography, like leylines if there were strict rules around how they moved and interacted. A wizard must rest or study within a place that is currently "on" to regain their spells in the traditional way.
"Well that sounds needlessly complex, Mr. Mann, why the hell would you want to do that? You could just make a pattern rotate on a clock and call it done!"
There are a few reasons!
A Few Reasons
The simple rules of Conway's Game of Life mean that anyone could pick them up and understand them pretty simply. In the world, these rules could eventually be discovered through experimentation. If the rules are understood, you can reliably predict when and where certain patterns will emerge so you can charge your spells. A wizard would have to collect and update their understanding of the patterns of magic that exist across the game world. That's interesting play! Scrounging around the ruins of the magicians of old for fundamental texts (that are gameable, no less) to create a chart of when and where to refill your biological wizard battery is the type of play I'm after!
Even if you aren't into that, though, there's still another aspect of gameplay in this system.
In the standard version of Conway's Game of Life, there are patterns called "oscillators" which cycle through a set number of states and are completely stable without any outside interference. In a wizardly world where magic is based around Conway's Game of Life, oscillators would become incredibly important, often home to wizard towers and colleges that utilize the consistent source of magic for their experiments.
What happens if an evil wizard wants to disrupt the oscillators?
Let's say there's a ritual that can be performed that flips a square in the map "on", or "off" if it's already on. Even one square missing from the pattern of an oscillator completely destroys it within a few states.
Suddenly, the domain play of wizards is centered around oscillators! Secret missions across the map to turn off the rival wizard's oscillators, constant ritual magics to try and maintain your own, the shenanigans that ensure are 1) obviously entertaining and a source of some very cool (gameable!) moments and 2) easily simulated and given the weight of consequence using the rules of Conway's Game of Life. You can directly affect the fabric of magic in a world as a player and as a referee it's as easy as clicking a button!
Oscillators aren't even the only possibility in Conway's Game of Life! There are "guns" which shoot "flyers" (projectiles) which can travel through the grid. Suddenly, the calm game of oscillators and agents becomes a mad dash to shoot waves of mana at your opponents and disrupt their constructions from across the game world! Conway's Game of Life is also Turing Complete (meaning it can simulate a Turing Machine, AKA a basic computer) so perhaps ancient civilizations built massive calculators or computers by utilizing the rules of Conway's Game of Life to manipulate magic. A fledgling wizard struggles to understand the machinations of magic. A master wizard shapes the flow of magic for the whole world.
The best part about all of this is that our nerds-in-arms over in the math department have already done a lot of the groundwork in regards to what is possible in Conway's Game of Life and some other nerds have already put up illustrations and GIFs of them over on the Wikipedia page for Conway's Game of Life.
There's one problem with all this: no one in the OSR uses square grids for their overworld! Nearly everyone who bothers to have an overworld map (and you certainly don't need one) slaps some hexes on that baby and calls it a day, and overlaying squares on hexes is icky-looking and doesn't bring me joy.
Thankfully, I was able to find this program made by Arun Arjunakani which is a type of cellular automata game made for hexes! The rules are unfortunately different from Conway's Game of Life (and may not possess some of the qualities I talked about above) but I encourage you to play around with it and see if you can get any cool patterns! Here are a few things I have found in about 30 minutes of tinkering around with the Hexagonal Game of Life:
A Few Shapes of Power
Here are 2 relatively small oscillators:
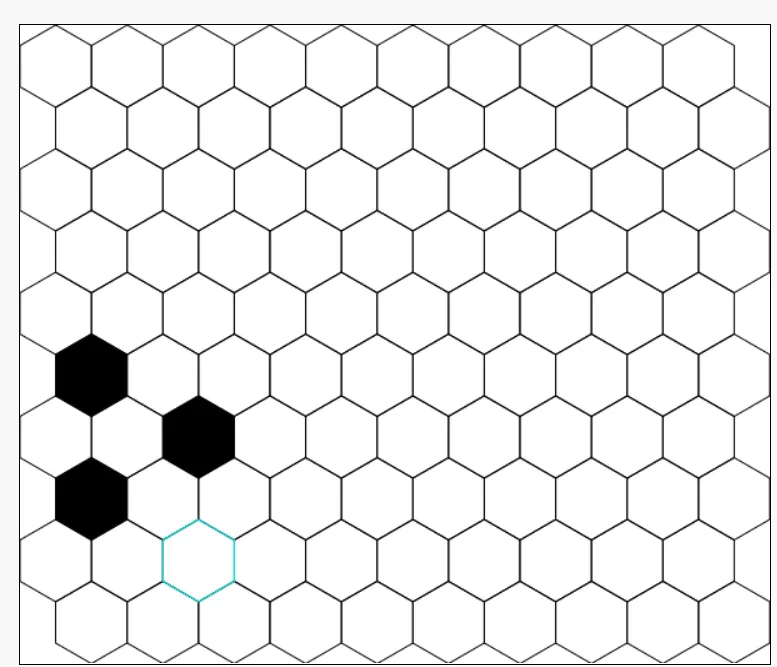
This one "rotates" in a triangular fashion around a central point, creating two unique stages. This one might be places around a Volcano, a lone mountain, or other cool, imposing singular hex.
I'm calling this a "maple seed oscillator" because its motion reminds me of a falling maple seed. The central hex stays stationary while its two "leaves" rotate along the vertical axis (i.e. they go right and left and right and left)
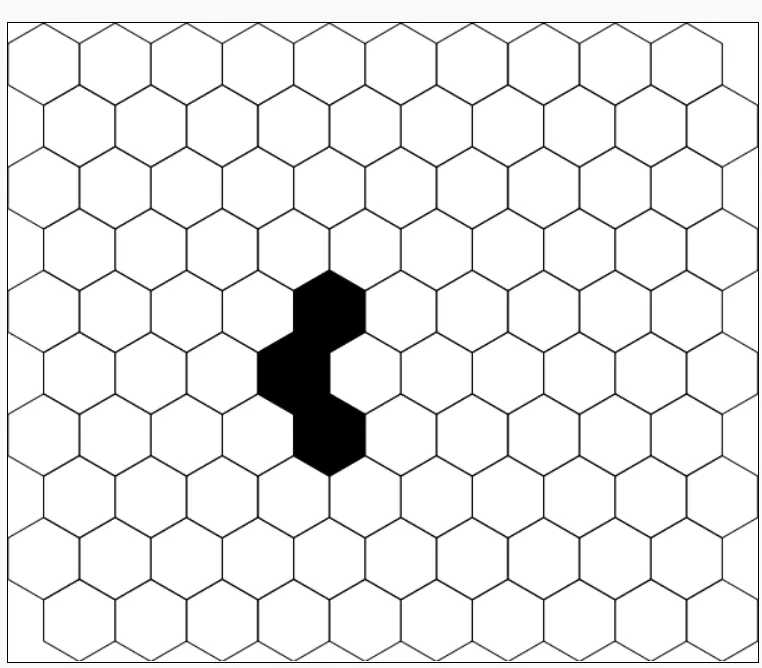
Here's the initial position of a larger oscillator:
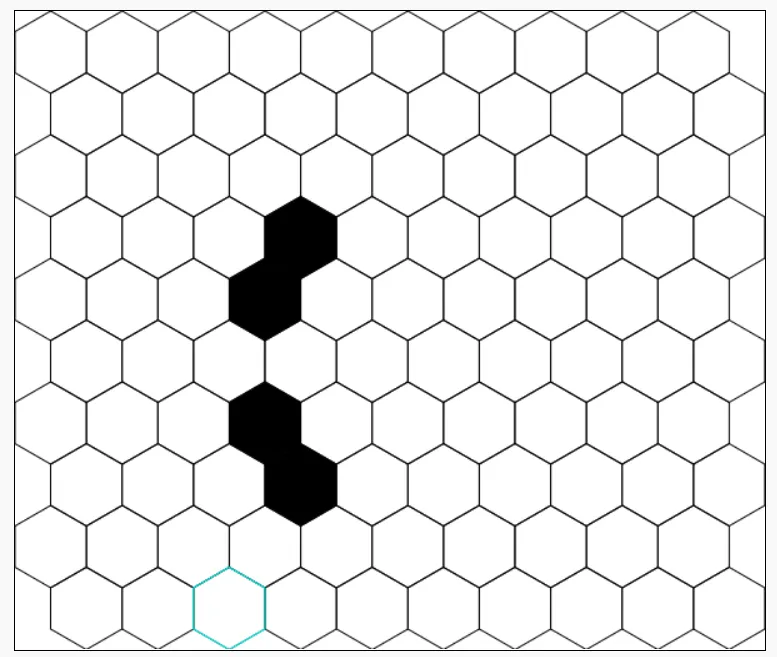
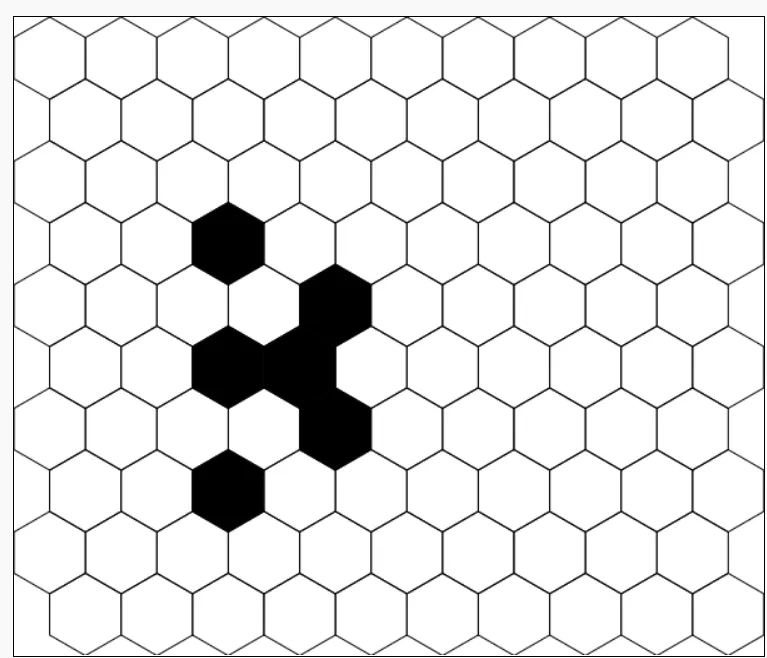
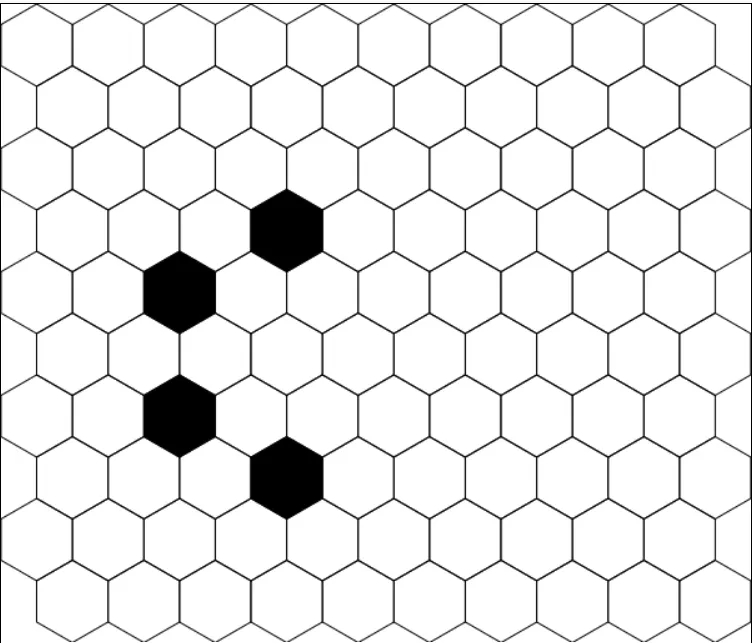
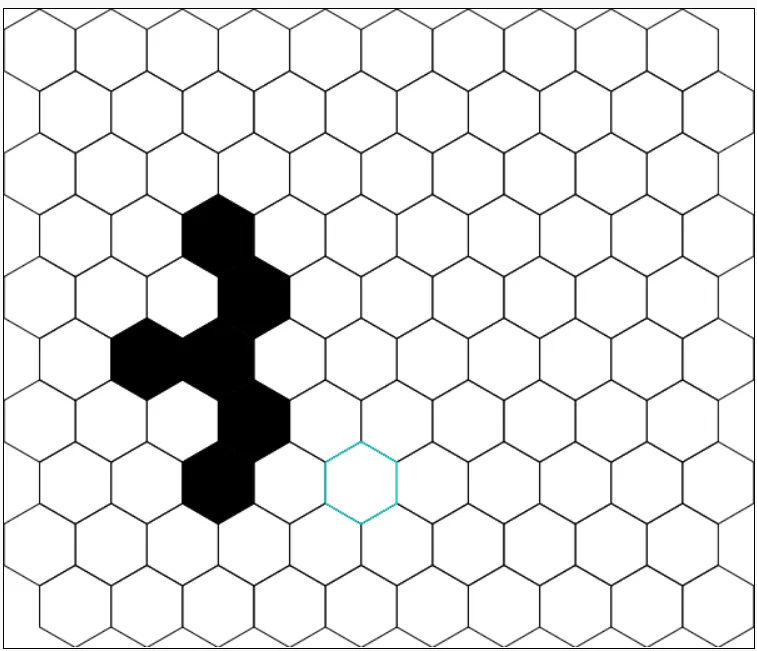
After the first revolution, the oscillator travels from the 2nd screenshot to the 5th screenshot and then repeats indefinitely.
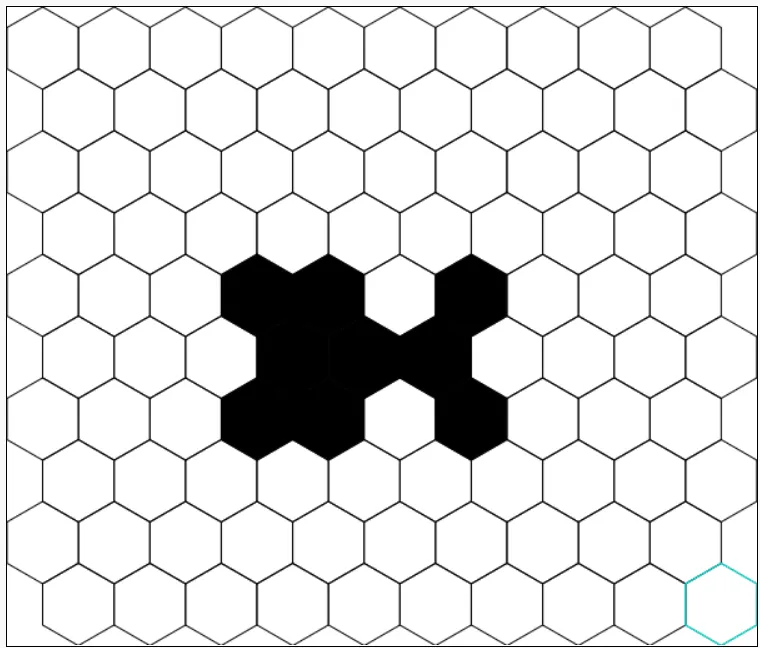
Now it's time to tell you about THE BOMB.
THE BOMB is a testament to the cold indifference of the universe of hexy magic. THE BOMB does not repeat, it is no pattern. THE BOMB spreads. It will cause a pattern of noise to spread out to at least a 100x100 hexmap (I sped up the simulation really fast).
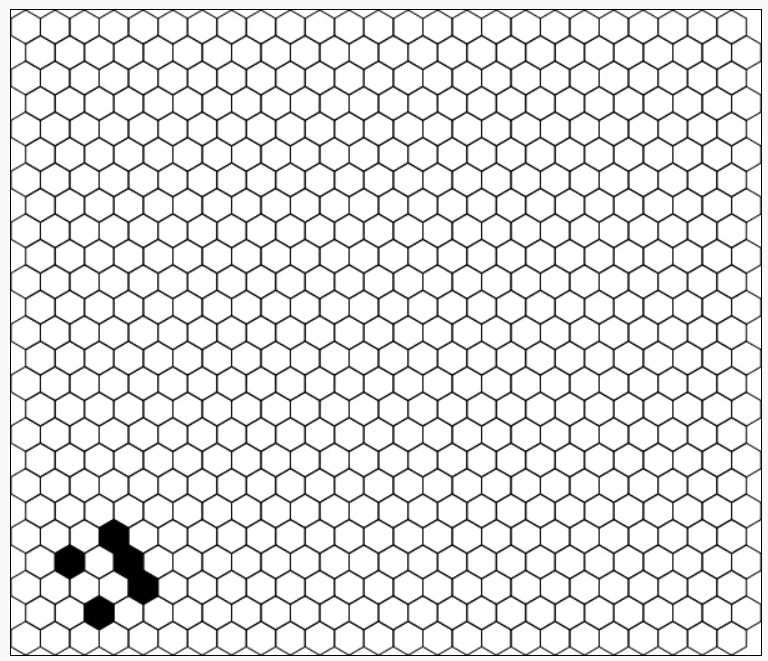

This is THE BOMB after 30 turns. It will spread. THE BOMB does not stop.
Not all patterns are evil, though! I found another one I've called "Yggdrasil" that's quite pretty:
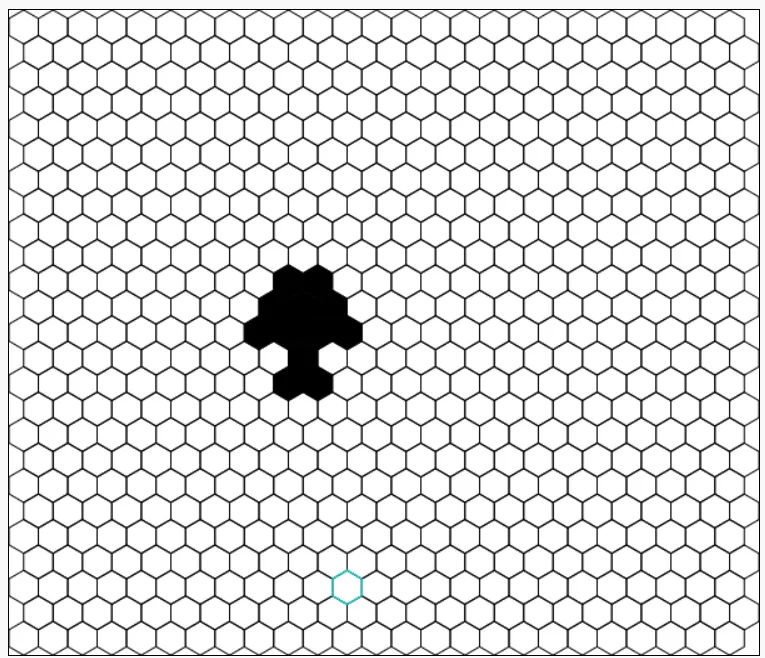
It maintains its symmetry for quite a while! here's a snapshot of the pattern around 10 turns:
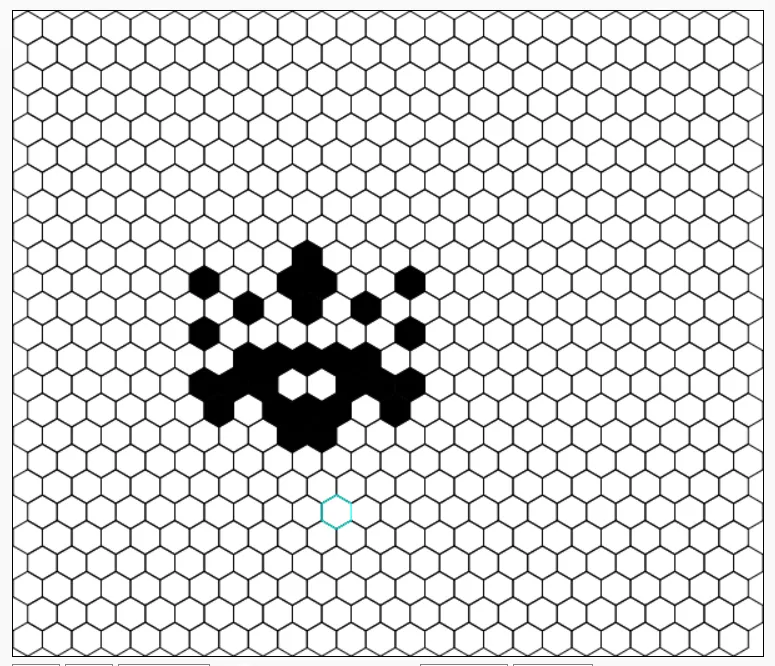
A bit later:
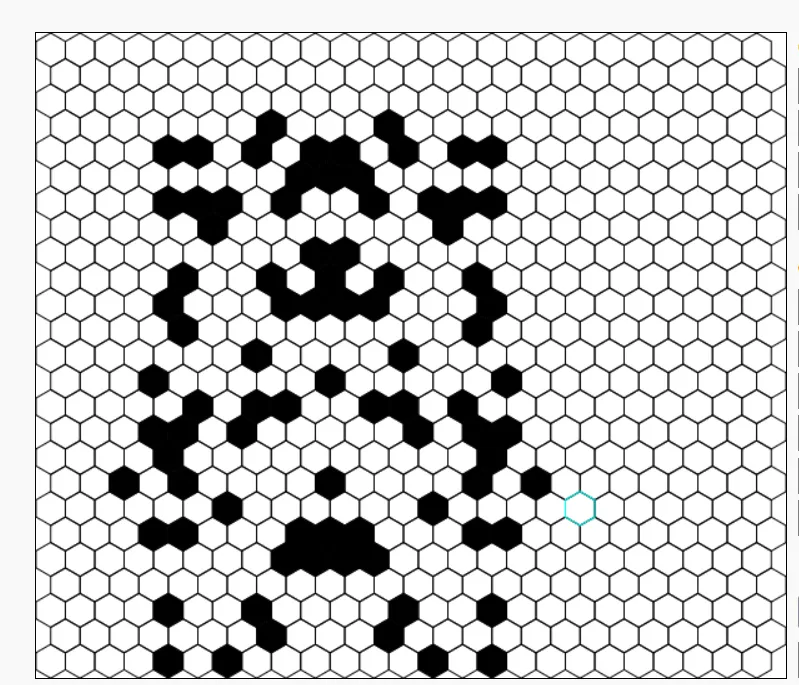
At some point, however, the nice symmetry of the pattern breaks, and THE BOMB begins to spread:
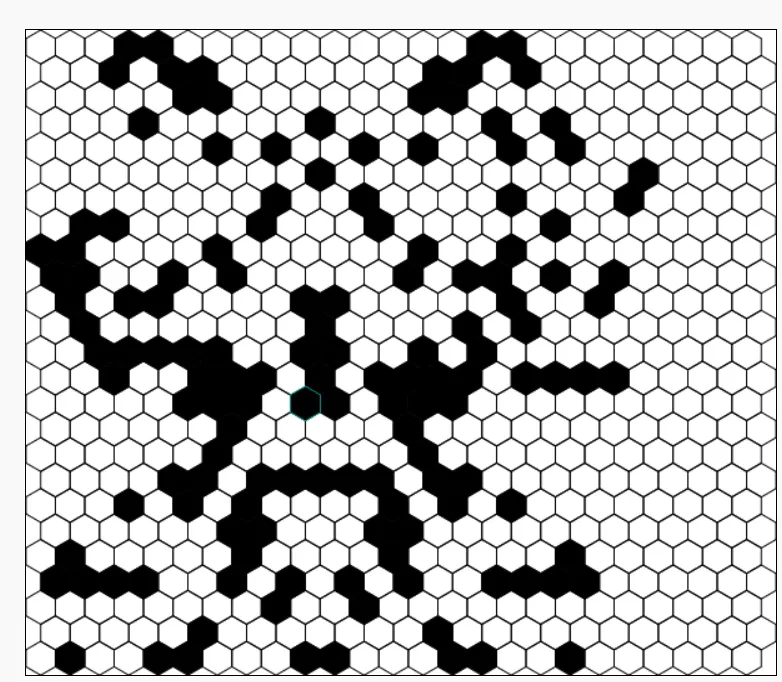
A Slapdash Set of Rules for Running Hexcrawls with the Hexagonal Game of Life
At the beginning of each day, advance the Game of Life simulation by one step. Wizards cannot regain spells if they do not spend the night resting in a hexagon that's "on".
The Ritual of Eximon
Assemble a large bowl with six sides. Paint each side a different color: Blue from the cobalt heart of a Rock Medusa, Green from the Chlorophyll of a Megafloral Cell, Quercitron Yellow, Brown ground from the robes of a mummy-lich, White from the bones of an ancient servitor, and Red from the aorta of a Dragon. Or maybe you don't need these things, but no one has figured that out yet.
Burn a beating heart in the center of the bowl. When the heart is naught but ash, split the bowl with an axe. The bowl strains against the axe blows, as if something is inside trying to free itself.
The hex this ritual is performs in changes its state the next time the simulation is advanced.